Tidal barrage operation optimization using moment-based control
DOI:
https://doi.org/10.36688/ewtec-2023-396Keywords:
Marine renewable energy, Tidal barrages, Optimal controlAbstract
As decarbonization of energy systems becomes an imperative and the deployment of intermittent renewables increases, the operation of electrical grids becomes challenging. In this sense, tidal barrage schemes can supply clean and predictable energy with more flexibility than the more traditional wind and solar plants. However, the high infrastructure costs associated with tidal barrage plants hinders its deployment. An optimal operation is key to maximize energy output and assure the project’s feasibility.Recently, Ringwood and Faedo [3] introduced a novel approach to tidal barrage control by applying wave energy control techniques, with promising results. The model consists on a two-way tidal barrage scheme, where an analogy is made between latching/declutching algorithms applied in WEC control and holding/sluicing from tidal barrage. The optimization was done using the moment-based framework developed in [1] and [2], which can formulate linear and non-linear problems in a concave quadratic environment, thus allowing the application of efficient numerical solution algorithms. This preliminary study has a number of simplifying assumptions, leaving a pathway to further examine the optimal control problem.
This paper extends the results of the analysis from [3] by adding complexities to the model. Crucially, the basin is modeled such as the area is a polynomial function of the water level, instead of assuming constant surface area. This will affect the operational head of the optimal solution, as the volume of water at the top of the basin will be higher than at the bottom. Another added constraint will be the minimum head that the turbine requires to generate electricity. Furthermore, a cost function is introduced to penalize the energy consumption of the sluice gates, as shown in figures 1.a) and 1.b). This not only increases the accuracy of the model, but in many cases improves the convergence of the algorithm by adding a quadratic term. Figure 2 shows the value of the overall energy yield (as a fraction of the energy output without penalty) and simulation run time (as a fraction of the run time without penalty) with different penalty coefficients.
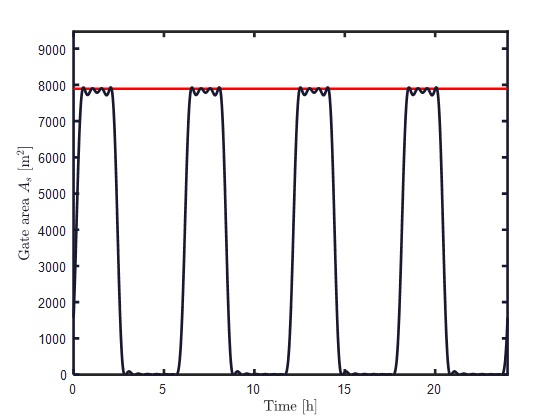 1.a) Sluice gate area without considering cost function
1.a) Sluice gate area without considering cost function
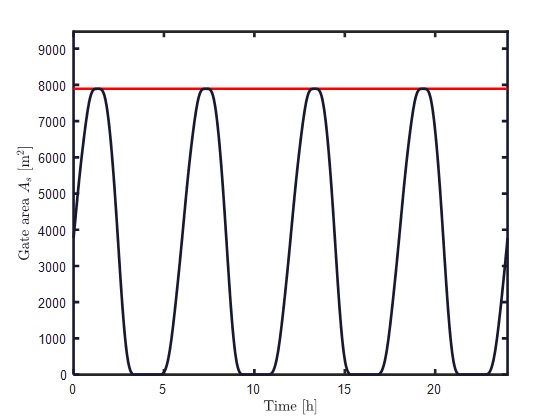 1.b) Sluice gate area with penalty factor of 3
1.b) Sluice gate area with penalty factor of 3
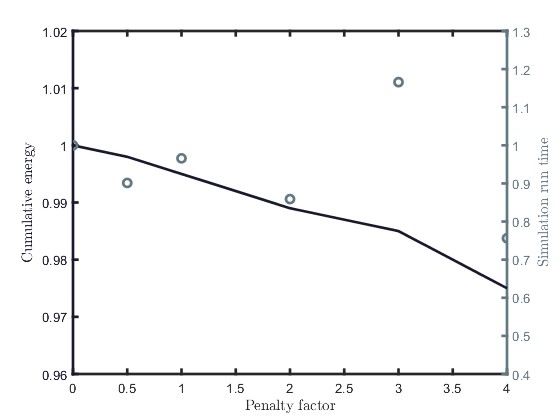 2. Energy and run time variations with penalty
References:
2. Energy and run time variations with penalty
References:[1] N. Faedo, G. Scarciotti, A. Astolfi, and J. V. Ringwood. Energy-maximising control of wave energy converters using a moment-domain representation. Control Engineering Practice, 81:85–96, 2018. [2] N. Faedo, G. Scarciotti, A. Astolfi, and J. V. Ringwood. Nonlinear energy-maximizing optimal control of wave energy systems: A moment-based approach. IEEE Transactions on Control Systems Technology, 29(6):2533–2547, 2021.
[3] J. V. Ringwood and N. Faedo. Tidal barrage operational optimisation using wave energy control techniques. IFAC-PapersOnLine, 55(31):148–153, 2022. 14th IFAC Conference on Control Applications in Marine Systems, Robotics, and Vehicles CAMS 2022.
Downloads
Published
2023-09-02
Issue
Track
Grid/off-grid integration, power take-off and control
Categories
License
Some rights reserved. Please see https://ewtec.org/proceedings/ for more details.
How to Cite
[1]
“Tidal barrage operation optimization using moment-based control”, Proc. EWTEC, vol. 15, Sep. 2023, doi: 10.36688/ewtec-2023-396.

